Chvorinov's rule
Chvorinov's Rule is a mathematical relationship first expressed by Nicolas Chvorinov in 1940[1], that relates the solidification time for a simple casting to the volume and surface area of the casting. In simple terms the rule establishes that under otherwise identical conditions, the casting with large surface area and small volume will cool more rapidly than a casting with small surface area and a large volume. The relationship can be written as:[2]
Where t is the solidification time, V is the volume of the casting, A is the surface area of the casting that contacts the mold, n is a constant, and B is the mold constant. The mold constant B depends on the properties of the metal, such as density, heat capacity, heat of fusion and superheat, and the mold, such as initial temperature, density, thermal conductivity, heat capacity and wall thickness. The metric units of the mold constant B are 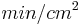 .[3] According to Askeland, the constant n is usually 2, however Degarmo claims it is between 1.5 and 2.[2][4] The mold constant of Chvorinov's rule, B, can be calculated using the following formula:
.[3] According to Askeland, the constant n is usually 2, however Degarmo claims it is between 1.5 and 2.[2][4] The mold constant of Chvorinov's rule, B, can be calculated using the following formula:
Where
- Tm = melting or freezing temperature of the liquid
- To = initial temperature of the mold
- ΔTs = Tpour − Tm = superheat
- L = latent heat of fusion
- k = thermal conductivity of the mold
- ρ = density of the mold
- c = specific heat of the mold
- ρm = density of the metal
- cm = specific heat of the metal
It is most useful in determining if a riser will solidify before the casting, because if the riser solidifies first then it is worthless.[4]
References
Notes
Bibliography
- Askeland, Donald R., and Phule, Pradeep P. Essentials of Materials Science and Engineering. Thomson, Ontario, Canada: 2004.
- Degarmo, E. Paul; Black, J T.; Kohser, Ronald A. (2003), Materials and Processes in Manufacturing (9th ed.), Wiley, ISBN 0-471-65653-4.
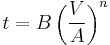
![B = \left[ \frac{\rho_m L}{ \left( T _m-T_o \right )} \right ]^2 \left[ \frac{\pi }{4 k \rho c} \right] \left[ 1 %2B \left( \frac{c_m \Delta T_s}{L} \right)^2 \right]](/2012-wikipedia_en_all_nopic_01_2012/I/b791fdf29de04a0d21128d8bb9819985.png)